Statistical forecasting: notes on regression and time series analysis
My notes and highlights on the book.
Author: Robert Nau
“This web site contains notes and materials for an advanced elective course on statistical forecasting that is taught at the Fuqua School of Business, Duke University. It covers linear regression and time series forecasting models as well as general principles of thoughtful data analysis.”
Table of Contents
- Table of Contents
- 1. Get to know your data
- 2. Introduction to forecasting: the simplest models
- 3. Averaging and smoothing models
- 4. Linear regression models
- 5. ARIMA models for time series forecasting
- What ARIMA stands for
- ARIMA models put it all together
- Construction of an ARIMA model
- ARIMA terminology
- Do you need both AR and MA terms?
- Interpretation of AR terms
- Interpretation of MA terms
- Tools for identifying ARIMA models: ACF and PACF plots
- AR and MA “signatures”
- Model-fitting steps
- Technical issues
- Seasonal ARIMA models
- Bottom-line suggestion
- Take-aways
- Seasonal differencing in ARIMA models
- Summary of rules for identifying ARIMA models
- 6. Choosing the right forecasting model
“I have seen the future and it is very much like the present, only longer.” – Kehlog Albran, The Profit
1. Get to know your data
Principles and risks of forecasting
Statistical forecasting: art and science of forecasting from data, with or without knowing in advance what equation you should use
Signal vs. noise
Variable you want to predict = signal + noise
- Signal: predictable component
- Noise: what is left over
Sensitive statistical tests are needed to get a better idea of whether the pattern you see in the data is really random or whether there is some signal yet to be extracted. If you fail to detect a signal that is really there, or falsely detect a signal that isn’t really there, your forecasts will be at best suboptimal and at worst dangerously misleading
random walk model: the variable takes random steps up and down as it goes forward:
- if you transform by taking the period-to-period changes (the “first difference”) it becomes a time series that is described by the mean model
- the confidence limits for the forecasts gets wider at longer forecast horizons
- typical of random walk patterns -> they don’t look random as they are! -> analyze the statistical properties: momentum, mean-reversion, seasonality
Risks of forecasting
“If you live by the crystal ball you end up eating broken glass”
- Intrinsic risk: random variation beyond explanation with the data and tools available
- Parameter risk: errors in estimating the parameters of the forecasting model, under the assumption that you are fitting the correct model to the data in the first place
When predicting time series, more sample data is not always better -> might include older data that is not as representative of current conditions. Blur of history problem: no pattern really stays the same forever
You can’t eliminate instrinsic risk and parameter risk, you can and should try to quantify them in relative terms -> so the appropriate risk-return tradeoffs can be made when decisions are based on the forecast
- Model risk: risk of choosing the wrong model. Most serious form of forecast error -> can be reduced by following good statistical practices: Follow good practices for exploring the data, understand the assumptions that are behind the models and test the assumptions.
If the errors are not pure noise -> there is some pattern in them, and you could make them smaller by adjusting the model to explain that pattern
Get to know your data
- Where did it come from?
- Where has it been?
- Is it clean or dirty?
- In what units is it measured?
Assembling, cleaning, adjusting and documenting the units of the data is often the most tedious step of forecasting
PLOT THE DATA!
You should graph your data to get a feel for its qualitative properties -> your model must accommodate these features and ideally it should shed light on their underlying causes
Inflation adjustment (“deflation”)
Accomplished by dividing a monetary time series by a price index, such as the Consumer Price Index (CPI) -> uncover the real growth
- original series: “nominal dollars” or “current dollars”
- deflated series: “constant dollars”
Not always necessary, sometimes forecasting the nominal data or log transforming for stabilizing the variance is simpler
Inflation adjustment is only appropriated for money series. If a non-monetary series shows signs of exponential growth or increasing variance -> try a logarithm transformation
Seasonal adjustment
Multiplicative adjustment
Increasing amplitude of seasonal variations is suggestive of a multiplicative seasonal pattern -> can be removed by multiplicative seasonal adjustment: dividing each value of the time series by a seasonal index that is representative of normal typically observed in that season
Additive adjustment
For time series whose seasonal variations are roughly constant in magnitude, independent of the current average level of the series -> adding or subtracting a quantity that represents the absolute amount by which the value in that season of the year tends to be below or above normal, as estimated from past data
Additive seasonal patterns are somewhat rare, but if applying log transform -> you should use additive rather than multiplicative
Acronyms
- SA: seasonally adjusted
- NSA: not seasonally adjusted
- SAAR: seasonally adjusted annual rate -> each period’s value has been adjusted for seasonality and then multiplied by the number of periods in a year, as though the same value had been obtained in every period for a whole year
Stationarity and differencing
Statistical stationarity
A stationary time series is one whose statistical properties such as mean, variance, autocorrelation, etc. are all constant over time. Most statistical forecasting methods are based on the assumption that the time series can be rendered approximately stationary (i.e., “stationarized”) through the use of mathematical transformations
- trend-stationary: series has a stable long-run rend and tends to revert to the trend line following a disturbance -> to stationarize it = detrending
- difference-stationary: if the mean, variance, and autocorrelations of the original series are not constant in time, even after detrending, perhaps the statistics of the changes in the series between periods or between seasons will be constant
Unit root test: to understand if a series is trend-stationary or difference-stationary
First-difference
Series of changes from one period to the next
- random walk model: if first-difference of a series is stationary and also completely random (not autocorrelated)
- ETS or ARIMA: can be used when the first-difference of a series is stationary but not completely random (its value at period t is autocorrelated with its value at earlier periods)
The logarithm transformation
Change in natural log ≈ percentage change
Small changes in the natural log of a variable are directly interpretable as percentage changes to a very close approximation
Linearization of exponential growth and inflation
The log transformation converts the exponential growth pattern to a linear growth pattern, and it simultaneously converts the multiplicative (proportional-variance) seasonal pattern to an additive (constant-variance) seasonal pattern
Logging a series often has an effect very similar to deflating: it straightens out exponential growth patterns and reduces heteroscedasticity (i.e., stabilizes variance). Logging is therefore a “poor man’s deflator” which does not require any external data
Geometric random walk: logging the data before fitting a random walk model -> commonly used for stock price data
Trend measured in natural-log units ≈ percentage growth
Usually the trend is estimated more precisely by fitting a statistical model that explicitly includes a local or global trend parameter, such as a linear trend or random-walk-with-drift or linear exponential smoothing model. When a model of this kind is fitted in conjunction with a log transformation, its trend parameter can be interpreted as a percentage growth rate.
Errors measured in natural-log units ≈ percentage errors
If you look at the error statistics in logged units, you can interpret them as percentages if they are not too large – if the standard deviation is 0.1 or less
Coefficients in log-log regressions ≈ proportional percentage changes
In many economic situations (particularly price-demand relationships), the marginal effect of one variable on the expected value of another is linear in terms of percentage changes rather than absolute changes
2. Introduction to forecasting: the simplest models
Review of basic statistics and the simplest forecasting model: the sample mean
Historical sample mean (or constant model, or intercept-only regression): if the series consists of i.i.d. values, the sample mean should be the next value if the goal is to minimize MSE
Why squared error?
- the central value around which the um of squared deviations are minimized is the sample mean
- variances are additive when random variables that are statistically independent are added together
- large errors often have disproportionately worse consequences than small errors, hence the squared error is more representative of the economic consequences of error
- variances and covariances play a key rola in normal distribution theory and regression analysis
nonlinear transformations of the data (e.g., log or power transformations) can often be used to turn skewed distributions into symmetric (ideally normal) ones, allowing such data to be well fitted by models that focus on mean values.
Fundamental law of forecasting risk
Variance of forecasting risk =
variance of intrinsic risk +
variance of parameter risk
Confidence intervals: sort like a probability, but not exactly -> there’s an x% probability that your future data will fall in your x% confidence interval for the forecast
Confidence interval =
forecast ±
(critical t-value) × (standard error of forecast)
95% confidence interval is (roughly) the forecat “plus-or-minus two standard errors”
A rule of thumb: when adjusted R-squared is fairly small (say, less than 20%), the percentage by which the standard error of the regression model is less than the standard error of the mean model is roughly one-half of adjusted R-squared.
t-stats, P-values, and R-squared, and other test statistics are numbers you should know how to interpret and use, but they are not the most important numbers in your analysis and they are not the bottom line:
- what new things have you learned from your data?
- what assumptions does your model make?
- would these assumptions make sense to someone else?
- would a simpler model perform almost as well?
- how accurate are your model’s predictions?
- how accurate it is likely to be to predict the future?
- how good are the inferences and decisions?
Notes on the random walk model
Model assumes that in each period the variable takes a random step away from its previous value, and the steps are independently and identically distributed in size (“i.i.d.”). This is equivalent to saying that the first difference of the variable is a series to which the mean model should be applied.
if you begin with a series that wanders all over the map, the first difference looks i.i.d. sequence -> random walk model is a potentially good candidate
- without drift: all future values will equal the last observed value
- with drift: the average increase from one period to the next (estimated drift = slope = d)
Square root of time rule: The confidence interval for a k-period-ahead random walk forecast is wider than that of a 1-period-ahead forecast by a factor of square-root-of-k
Are the daily changes statistically independent as well having a mean of zero? autocorrelation plot -> random walk without drift
The geometric random walk model
The natural logarithm of the variable is assumed to walk a random walk, usually with drift
Diff-logs are interpretable as (approximate) percentage changes
it is very hard to estimate the trend in a random-walk-with-drift model based on the mean growth that was observed in the sample of data unless the sample size is very large
Fitting a random-walk-with-drift model to the logged series is equivalent to fitting the geometric random walk model to the original series.
Reasons for using the random walk model
- If you see what looks like pure noise (i.i.d. variations) after performing a 1st -difference or diff-log transformation, then your data is telling you that you that it is a random walk. This isn’t very exciting in terms of the point forecasts you should make (“next month will be the same as last month, plus average growth”), but it has very important implications in terms of how much uncertainty there is in forecasting more than one period ahead.
- benchmark against which to compare more complicated time series models, particularly regression models
Mean (constant) model
Predicting a variable whose values are i.i.d.
Sample mean: by definition an unbiased predictor and minimizes the mean squared forecasting error regardless of the probability distribution -> it is the value around which the sum of squared deviations of the sample data is minimized
Standard error of the mean: how accurate is the estimate of the sample mean -> equals the sample stdev divided by the sqrt of the sample size
Central limit theorem -> large samples: 95% confidence interval = mean +- 2*stdev
Standard error of the forecast: equal to the sample stdev * sqrt(1+1/n)
Confidence interval for a forecast is the point forecast plus-or-minus the appropriate critical t-value times the standard error of the forecast
The critical t-value for a 50% confidence interval is approximately 2/3, so a 50% confidence interval is one-third the width of a 95% confidence interval. The nice thing about a 50% confidence interval is that it is a “coin flip” as to whether the true value will fall inside or outside of it, which is extremely easy to think about
If we can find some mathematical transformation (e.g., differencing, logging, deflating, etc.) that converts the original time series into a sequence of values that are i.i.d., we can use the mean model to obtain forecasts and confidence limits for the transformed series, and then reverse the transformation to obtain corresponding forecasts and confidence limits for the original series.
Linear trend model
aka trend-line model: special case of a simple regression model in which the independent variable is just a time index variable.
R-squared = 0.143 -> the variance of the regression model’s errors is 14.3% less than the variance of the mean model’s errors, i.e., the model has “explained” 14.3% of the variance in the series
If the model has succeeded in extracting all the “signal” from the data, there should be no pattern at all in the errors: the error in the next period should not be correlated with any previous errors:
- lag-1 autocorrelation: should be very close to zero
- Durbin-Watson statistic: ought to be very close to 2
trend lines have their use as visual aids, but are often poor for forecasting
Random walk model
Time series with irregular growth -> predict the change from one period to the next (first difference)
autocorrelation at lag k -> correlation between the variable and itself lagged by k periods
- random-walk-without-drift: assumes that at each point, the series merely takes a random step away from its last recorded position, with steps whose mean value is zero -> values of the autocorrelations are not significantly different than zero (95% confidence interval), no change from one period to the next, because past data provides no information about the direction of future movements
- random-walk-with-drift: mean step size is some nonzero value
In the random-walk-without-drift model, the standard error of the 1-step ahead forecast is the root-mean-squared-value of the period-to-period changes
For a random-walk-with-drift, the forecast standard error is the sample standard deviation of the period-to-period changes.
“Square root of time” rule for the errors of random walk forecasts: the standard error of a k-step-ahead forecast is larger than that of the 1-step-ahead forecast by a factor of square-root-of-k. This explains the sideways-parabola shape of the confidence bands for long-term forecasts.
Random walk may look trivial -> naive model (always predict that tomorrow will be the same as today). The square-root-of-time pattern in its confidence bands for long-term forecasts is of profound importance in finance (it is the basis of the theory of options pricing), and the random walk model often provides a good benchmark against which to judge the performance of more complicated models
RWM -> special case of an ARIMA model -> ARIMA(0, 1, 0)
Geometric random walk model
Natural logarithm transformation: linearize exponential growth and stabilize variance of changes (“diff-log”)
It can be dangerous to estimate the average rate of return to be expected in the future (let alone anticipate short-term changes in direction), by fitting straight lines to finite samples of data!
Geometric random walk model: Application of the random walk model to the logged series implies that the forecast for the next month’s value of the original series will equal the previous month’s value plus a constant percentage increase.
In unlogged units, the 95% confidence limits for long-term forecasts are noticeably asymmetric
More general random walk forecasting models
- RW model 1: basic geometric random walk -> assumes series in different periods are statistically independent (uncorrelated) and also identically distributed
- RW model 2: assumes the series in different periods are statistically independent but not identically distributed
- RW model 3: assumes that returns in different periods are uncorrelated but not otherwise independent. The ARCH (autoregressive conditional heteroscedasticity) and GARCH (generalized ARCH) models assume that the local volatility follows an autoregressive process, which is characterized by sudden jumps in volatility with a slow reversion to an average volatility
Three types of forecasts: estimation, validation, and the future
Out-of-sample validation: withhold some of the sample data from the model identification and estimation process, then use the model to make predictions for the hold-out data to see how accurate they are and to determine whether the statistics of their errors are similar to those that the model made within the sample of data that was fitted
Overfitting (likely when):
- model with a large number of parameters fitted to a small sample of data
- model has been selected from a large set of potential models precisely by minimizing the MSE in the estimation period
Backtests: one-step-ahead forecasts in the validation period (held out during parameter estimation)
If you test a great number of models and choose the model whose errors are smallest in the validation period, you may end up overfitting the data within the validation period as well as in the estimation period
- Holding data out for validation purposes is probably the single most important diagnostic test of a model: it gives the best indication of the accuracy that can be expected when forecasting the future
- When you’re ready to forecast the future in real time, you should of course use all the available data for estimation, so that the most recent data is used
Forecasts into the future are “true” forecasts that are made for time periods beyond the end of the available data
The model with the tightest confidence intervals is not always the best model -> a bad model not always know it is a bad model
3. Averaging and smoothing models
Simple moving averages
- mean model: best predictor of tomorrow is the avg of everything that has happened until now
- random walk model: best predictor of tomorrow is what happened today, ignoring previous history
- moving average: take an average of what has happened in some window of the recent past
moving average model: superior to the mean model in adapting to cyclical pattern and superior to the random walk model in not being too sensitive to random shocks from one period to the next
Simple moving average (SMA):
- Each of the past m observations gets a weight of
1/min the averaging formula, so asmgets larger, each individual observation in the recent past receives less weight. This implies that larger values ofmwill filter out more of the period-to-period noise and yield smoother-looking series of forecasts - average age of the data in the forecast is
(m+1)/2-> amount by which the forecasts will tend to lag behind in trying to follow trends or respond to turning points
Value of
mtradeoff: filtering out more noise vs. being too slow to respond to trends and turning points
Comparing measures of forecast error between models
- RMSE: root mean squared error: (the most common standard of goodness-of-fit, penalizes big errors relatively more than small errors because it squares them first; it is approximately the standard deviation of the errors if the mean error is close to zero)
- MAE: mean absolute error (the average of the absolute values of the errors, more tolerant of the occasional big error because errors are not squared)
- MAPE: mean absolute percentage error (perhaps better to focus on if the data varies over a wide range due to compound growth or inflation or seasonality, in which case you may be more concerned about measuring errors in percentage terms)
- ME: mean error (this indicates whether forecasts are biased high or low—should be close to 0)
- MPE: mean percentage error (ditto in percentage terms)
Best measure for size of error = RMSE
Easier for non-specialists to understand = MAE and MAPE
SMA with a trend = SMD + drift (add a constant to the SMA forecasting equation)
Tapered Moving Average: put only half as much weight on the newest and oldest values -> more robust to outliers in the data
Simple exponential smoothing
SMA problems:
- putting equal weight on the last m observations and no weight on any previous observations is usually not the best way to average values that are arriving consecutively in time
- would make more sense to gradually decrease the weights placed on the older values
- its confidence intervals for long-horizon forecasts do not widen at all
Simple exponential smoothing (SES) aka Exponentially weighted moving average model: addresses these shortcomings of SMA
most used time series model in business applications:
- good forecast under a wide range of conditions
- computationally it is extremely simple
the SES model is an interpolation between the mean model and the random walk model with respect to the way it responds to new data. As such it might be expected to do better than either of them in situations where the random walk model over-responds and the mean model under-responds, and indeed it does
Overall the SES model is superior to the SMA model in responding a bit more quickly to the newest data while treating older data more even-handedly, when the models otherwise yield the same average age
all models are based on assumptions about how the world works, and you need to understand what the assumptions are and (ideally) you should believe in the assumptions of your chosen model and be able to explain and defend them.
Linear Exponential Smoothing (LES)
Generalization of the SES to obtain a model that computes local estimates of both level and trend -> same basic logic, but now you have two smoothing constants, one for the level and one for the trend
Any smoothing model will lag behind to some extent in responding to unforeseen changes in level or trend
many time series that arise in business and economics (as well as engineering and the natural sciences) which are inherently non-seasonal or which have been seasonally adjusted display a pattern of random variations around a local mean value or a local trend line that changes slowly with time. The first difference of such a series is negatively autocorrelated at lag 1: a positive change tends to be followed by a (smaller) negative one. For time series of this type, a smoothing or averaging model is the appropriate forecasting model.
Out-of-sample validation
Aka “backtesting”: holding out some of the data while estimating parameters of alternative models, then freezing those parameter estimates and using them to make predictions for the hold-out data
You hope to find the statistics of the errors of the predictions for the hold-out data look very similar to those of the predictions for the sample data
If the data exhibits exponential growth due to compounding or inflation, then it will display greater volatility in absolute terms toward the end of the series, even if the volatility is constant in percentage terms. In situations like this you may want to use a nonlinear transformation such as logging or deflating as part of your model
it is usually best to look at MAPE’s rather than RMSE’s when asking whether a given model performed about as well in the validation period as in the estimation period.
Moving average and exponential smoothing models
Moving beyond mean models, random walk models, and linear trend models, nonseasonal patterns and trends can be extrapolated using a moving-average or smoothing model.
Which type of trend-extrapolation is best: horizontal or linear? Empirical evidence suggests that, if the data have already been adjusted (if necessary) for inflation, then it may be imprudent to extrapolate short-term linear trends very far into the future. Trends evident today may slacken in the future due to varied causes such as product obsolescence, increased competition, and cyclical downturns or upturns in an industry. For this reason, simple exponential smoothing often performs better out-of-sample than might otherwise be expected, despite its “naive” horizontal trend extrapolation. Damped trend modifications of the linear exponential smoothing model are also often used in practice to introduce a note of conservatism into its trend projections.
Forecasting with adjustments for inflation and seasonality
- Deflation with prices indices
- Seasonal decompositon
- Time series forecasting models for seasonal data
- Averaging and smoothing combined with seasonal adjustment
- Winters seasonal exponential smoothing model
Modeling the effect of inflation
Why?
- to measure real growth and estimate its dependence on other real factors
- to remove much of the trend and stabilize variance before fitting the model
How?
- to “deflate” a variable, you divide it by an appropriate price index variable
- e.g.: general price index, product-specific index
- to “re-inflate” forecasts of a deflated series, you multiply the forecasts and confidence limits by a forecast of the price index
Log vs. deflate
- Deflation should be used when you are interested in knowing the forecast in “real” terms and/or if the inflation rate is expected to change
- Logging is sufficient if you just want a forecast in “nominal” terms and inflation is expected to remain constant—inflation just gets lumped with other sources of compound growth in the model.
- Logging also ensures that forecasts and confidence limits have positive values, even in the presence of downward trends and/or high volatility.
- If inflation has been minimal and/or there is little overall trend or change in volatility, neither may be necessary
Seasonality
- repeating, preiodic pattern in the data that is keyed to the calendar of the clock
- != than “cyclality”, which do not have a predictable periodicity
Seasonal patterns are complex, because the calendar is not rational: months and years don’t have whole numbers of weeks, a given month does not always have the same number of trading days/weekends, Christmans day can fall on any day of the week, some major holidays are “moveable feasts” that do not occur on the same calendar dates each year
- Quarterly data is easiest to handle: 4 quarters in a year, 3 months in a quarter, trading day adjustments have only minor effects.
- Monthly data is more complicated: 12 months in a year, but not 4 weeks in a month; trading day adjustments may be important.
- Weekly data requires special handling because a year is not exactly 52 weeks.
Multiplicative seasonality
Most natural seasonal patterns are multiplicative
- Seasonal variations are roughly constant in percentage terms
- Seasonal swings get larger or smaller in absolute magnitude as the average level of the series rises or falls due to long-term trends and/or business cycle effects
Additive seasonality
Additive seasonal pattern has constant-amplitude seasonal swings in the presence of trends and cycles.
- A log transformation converts a multiplicative pattern to an additive one, so if your model includes a log transformation, use additive rather than multiplicative seasonal adjustment.
- If the historical data sample has little trend and seasonal variations are not large in relative terms, additive and multiplicative adjustment yield very similar results
Seasonal index
- Represents the expected percentage of “normal” in a given month or quarter
- When the seasonal indices are assumed to be stable over time, they can be estimated by the “ratio to moving average” (RMA) method
Winters’ Seasonal Smoothing
The logic of Holt’s LES model can be extended to recursively estimate time-varying seasonal indices as well as level and trend.
Issues:
- Estimation of Winters’ model is tricky
- There are three separate smoothing constants to be jointly estimated by nonlinear least squares.
- Initialization is also tricky, especially for the seasonal indices.
- Confidence intervals sometimes come out extremely wide because the model “lacks confidence in itself.”
In practice:
- The Winters model is popular in “automatic forecasting” software, because it has a little of everything (level, trend, seasonality).
- Often it works very well, but difficulties in initialization & estimation can lead to strange results in some cases.
- It responds to recent changes in the seasonal pattern as well as the trend, but with some danger of unstable long-term trend projections.
4. Linear regression models
Introduction to linear regression
Regression analysis: art and science of fitting straight lines to patterns of data
Assumptions:
- The expected value of Y is a linear function of the X variables
- The unexplained variations of Y are independent random variables (in particular, not “autocorrelated” if the variables are time series)
- The all have the same variance (“homoscedasticity”)
- They are normally distributed
No model is perfect - these assumptions will never be exactly satisfied by real-world messy data - but you hope that they are not badly wrong. The art of regression modeling is to (most importantly!) collect data that is relevant and informative with respect to your decision or inference problem, and then define your variables and construct your model in such a way that the assumptions listed above are plausible, at least as a first-order approximation to what is really happening
Correlation and regression-to-mediocrity
Regression-to-mediocrity aka regression to the mean: Purely statistical phenomenon that can be viewed as a form of selection bias. Every quantitative measurement is a combination of signal and noise. When a value above the mean is observed, it is probable that the value of the signal was above average and the value of the noise was above average. Now suppose there is some other quantity (say, some measurable trait of the offspring—not necessarily the same one) whose value depends only on the signal, not the noise, in the first quantity. Then a measurement of the second quantity should also be expected to be above the mean, but less so in relative terms, because only the above-average signal is passed on; the above-average noise is not. In fact, it is the independent noise in the second quantity that prevents variations from ever dying out over generations.
The coefficient of correlation between X and Y is the average product of their standardized values
It is a number that lies somewhere between -1 and +1, where -1 indicates a perfect negative linear relationship, +1 indicates a perfect positive linear relationship, and zero indicates no linear relationship.
A correlation of zero between X and Y does not necessarily mean that there is no relationship, just that there is no linear relationship within the historical sample of data that is being analyzed. e.g., y = xˆ2
When we speak of “regressing” one variable on a group of others, we mean the fitting of a linear equation that minimizes the sum of squared errors in predicting that variable from the others.
Mathematics of a regression model
- The coefficients and error measures for a regression model are entirely determined by the following summary statistics: means, standard deviations, and correlations of the variables, and the sample size
- The correlation between Y and X is equal to the average product of their standardized values
- The slope coefficient in a simple regression of Y on X is the correlation between Y and X multiplied by the ratio of their standard deviations
- In a simple regression model, the percentage of variance “explained” by the model, which is called R-squared, is the square of the correlation between Y and X
- The sample standard deviation of the errors is a downward-biased estimate of the size of the true unexplained deviations in Y because it does not adjust for the additional “degree of freedom” used up by estimating the slope coefficient
- Adjusted R-squared, which is obtained by adjusting R-squared for the degrees if freedom for error in exactly the same way, is an unbiased estimate of the amount of variance explained
- For models fitted to the same sample of the same dependent variable, adjusted R-squared always goes up when the standard error of the regression goes down. A model does not always improve when more variables are added: adjusted R-squared can go down (even go negative) if irrelevant variables are added
- The standard error of a coefficient estimate is the estimated standard deviation of the error in measuring it. And the estimated height of the regression line for a given value of X has its own standard error, which is called the standard error of the mean at X. All of these standard errors are proportional to the standard error of the regression divided by the square root of the sample size
- The standard error of the forecast for Y for a given value of X is the square root of the sum of squares of the standard error of the regression and the standard error of the mean at X
- Two-sided confidence limits for coefficient estimates, means, and forecasts are all equal to their point estimates plus-or-minus the appropriate critical t-value times their respective standard errors.
What to look for in regression model output
Standard error of the regression (root-mean-squared error adjusted for degrees of freedom)
It is a lower bound on the standard error of any forecast generated from the model
In time series forecasting, also common to look the mean absolute error (MAE) and, for positive data, the mean absolute percentage error (MAPE)
Mean absolute scaled error -> measures improvement in mean absolute error relative to a random-walk-without-drift model
Adjusted R-squared
R-squared (the fraction by which the variance of the errors is less than the variance of the dependent variable) adjusted for the number of coefficients in the model relative to the sample size in order to correct it for bias.
Adjusted R-squared is the fraction by which the square of the standard error of the regression is less than the variance of the dependent variable
Unitless statistic, but there is no absolute standard for what is a “good” value
Significance of the estimated coefficients
Are the t-statistics greater than 2 in magnitude, corresponding to p-values less than 0.05? If they are not, you should probably try to refit the model with the least significant variable excluded, which is the “backward stepwise” approach to model refinement.
Values of the estimated coefficients
In general you are interested not only in the statistical significance of an independent variable, you are also interested in its practical significance. In theory, the coefficient of a given independent variable is its proportional effect on the average value of the dependent variable, others things being equal -> “bang for the buck”.
Plots of forecasts and residuals
DO NOT FAIL TO LOOK AT PLOTS OF THE FORECASTS AND ERRORS. Do the forecasts “track” the data in a satisfactory way, apart from the inevitable regression-to-the mean? (In the case of time series data, you are especially concerned with how the model fits the data at the “business end”, i.e., the most recent values.) Do the residuals appear random, or do you see some systematic patterns in their signs or magnitudes? Are they free from trends, autocorrelation, and heteroscedasticity? Are they normally distributed? There are a variety of statistical tests for these sorts of problems, but the best way to determine whether they are present and whether they are serious is to look at the pictures.
Out-of-sample validation
A good model should have small error measures in both the estimation and validation periods, compared to other models, and its validation period statistics should be similar to its own estimation period statistics. Regression models with many independent variables are especially susceptible to overfitting the data in the estimation period, so watch out for models that have suspiciously low error measures in the estimation period and disappointingly high error measures in the validation period.
Be aware that if you test a large number of models and rigorously rank them on the basis of their validation period statistics, you may end up with just as much “data snooping bias” as if you had only looked at estimation-period statistics–i.e., you may end up picking a model that is more lucky than good! The best defense against this is to choose the simplest and most intuitively plausible model that gives comparatively good results.
What’s the bottom line? How to compare models
After fitting a number of different regression or time series forecasting models to a given data set, you have many criteria by which they can be compared:
- Error measures in the estimation period: root mean squared error, mean absolute error, mean absolute percentage error, mean absolute scaled error, mean error, mean percentage error
- Error measures in the validation period (if you have done out-of-sample testing): Ditto
- Residual diagnostics and goodness-of-fit tests: plots of actual and predicted values; plots of residuals versus time, versus predicted values, and versus other variables; residual autocorrelation plots, cross-correlation plots, and tests for normally distributed errors; measures of extreme or influential observations; tests for excessive runs, changes in mean, or changes in variance (lots of things that can be “OK” or “not OK”)
- Qualitative considerations: intuitive reasonableness of the model, simplicity of the model, and above all, usefulness for decision making!
The bottom line is that you should put the most weight on the error measures in the estimation period–most often the RMSE, but sometimes MAE or MAPE–when comparing among models.
The MASE statistic provides a very useful reality check for a model fitted to time series data: is it any better than a naive model?
You may also want to look at Cp, AIC or BIC, which more heavily penalize model complexity. But you should keep an eye on the residual diagnostic tests, cross-validation tests (if available), and qualitative considerations such as the intuitive reasonableness and simplicity of your model.
K.I.S.S. (keep it simple…): If two models are generally similar in terms of their error statistics and other diagnostics, you should prefer the one that is simpler and/or easier to understand.
5. ARIMA models for time series forecasting
Auto-Regressive Integrated Moving Average
What ARIMA stands for
- Series which needs to be differenced to be made stationary = an “integrated” (I) series
- Lags of the stationarized series are called “auto-regressive” (AR) terms
- Lags of the forecast errors are called “moving average” (MA) terms
ARIMA models put it all together
- Generalized random walk models fine-tuned to eliminate all residual autocorrelation
- Generalized exponential smoothing models that can incorporate long-term trends and seasonality
- Stationarized regression models that use lags of the dependent variables and/or lags of the forecast errors as regressors
- The most general class of forecasting models for time series that can be stationarized* by transformations such as differencing, logging, and or deflating
Construction of an ARIMA model
- Stationarize the series, if necessary, by differencing (& perhaps also logging, deflating, etc.)
- Study the pattern of autocorrelations and partial autocorrelations to determine if lags of the stationarized series and/or lags of the forecast errors should be included in the forecasting equation
- Fit the model that is suggested and check its residual diagnostics, particularly the residual ACF and PACF plots, to see if all coefficients are significant and all of the pattern has been explained.
- Patterns that remain in the ACF and PACF may suggest the need for additional AR or MA terms
ARIMA terminology
ARIMA(p,d,q) -> non-seasonal ARIMA:
p = number of autoregressive terms
q = number of non-seasonal differences
d = number of moving-average terms
Do you need both AR and MA terms?
- in general, you don’t
- If the stationarized series has positive autocorrelation at lag 1, AR terms often work best. If it has negative autocorrelation at lag 1, MA terms often work best.
- An MA(1) term often works well to fine-tune the effect of a nonseasonal difference, while an AR(1) term often works well to compensate for the lack of a nonseasonal difference, so the choice between them may depend on whether a difference has been used.
Interpretation of AR terms
Autoregressive (AR) behavior: apparently feels a “restoring force” that tends to pull it back toward its mean
Interpretation of MA terms
Moving average (MA) behavior: apparently undergoes random “shocks” whose effects are felt in two or more consecutive periods
Tools for identifying ARIMA models: ACF and PACF plots
- Autocorrelation function (ACF) plot: shows the correlation of the series with itself at different lags
- Partial autocorrelation function (PACF) plot: shows the amount of autocorrelation at lag
kthat is not explained by lower-order autocorrelations
AR and MA “signatures”
- ACF that dies out gradually and PACF that cuts off sharply after a few lags -> AR signature
- AR series is usually positive autocorrelated at lag 1
- ACF that cuts off sharply after a few lags and PACF that dies out more gradually -> MA signature
- MA series is usually negatively autocorrelated at lag 1
Whether a series displays AR or MA behavior often depends on the extent to which it has been differenced. “Underdifferenced” series -> AR signature (positive autocorrelation). After one or more orders of differencing, the autocorrelation will become more negative and an MA signature will emerge
Model-fitting steps
- Determine the order of differencing
- Determine the numbers of AR & MA terms
- Fit the model—check to see if residuals are “white noise,” highest-order coefficients are significant (w/ no “unit “roots”), and forecasts look reasonable. If not, return to step 1 or 2.
Technical issues
- Backforecasting: Estimation algorithm begins by forecasting backward into the past to get start-up values
- Unit roots: Look at sum of AR coefficients and sum of MA coefficients—if they are too close to 1 you may want to consider higher or lower of differencing
- Overdifferencing: A series that has been differenced one too many times will show very strong negative autocorrelation and a strong MA signature, probably with a unit root in MA coefficients
Seasonal ARIMA models
Rely on seasonal lags and differences to fit the seasonal pattern. Generalizes the regression approach.
Terminology
Seasonal part of an ARIMA model is summarized by three additional numbers:
- P = # of seasonal autoregressive terms
- D = # of seasonal differences
- Q = # of seasonal moving average terms
“ARIMA(p,d,q)x(P,D,Q)” model
P, D and Q should never be larger than 1
Model fitting steps
- Start by trying various combinations of one seasonal difference and/or one non-seasonal difference to stationarize the series and remove gross features of seasonal pattern.
- If the seasonal pattern is strong and stable, you MUST use a seasonal difference (otherwise it will “die out” in long-term forecasts)
- After differencing, inspect the ACF and PACF at
multiples of the seasonal period (s):
- Positive spikes in ACF at lag s, 2s, 3s…, single positive spike in PACF at lag s -> SAR=1
- Negative spike in ACF at lag s, negative spikes in PACF at lags s, 2s, 3s,… -> SMA=1
- SMA=1 often works well in conjunction with a seasonal difference.
Same principles as for non-seasonal models, except focused on what happens at multiples of lag
sin ACF and PACF.
Bottom-line suggestion
Strong seasonal pattern, try:
- ARIMA(0,1,q)x(0,1,1) model (q=1 or 2)
- ARIMA(p,0,0)x(0,1,1)+c model (p=1, 2 or 3)
- If there is a significant trend and/or the seasonal pattern is multiplicative, you should also try a natural log transformation.
Take-aways
- Advantages: solid underlying theory, stable estimation of time-varying trends and seasonal patterns, relatively few parameters.
- Drawbacks: no explicit seasonal indices, hard to interpret coefficients or explain “how the model works”, danger of overfitting or mis-identification if not used with care.
Seasonal differencing in ARIMA models
Seasonal difference: series of changes from one season to the next. i.e. 12 periods in a season -> seasonal difference = Y(t)-Y(t-12)
Usually removes the gross features of seasonality from a series, as well as most of the trend.
First difference of the seasonal difference = (Y(t)-Y(t-12))-(Y(t-1)-Y(t-13))
Summary of rules for identifying ARIMA models
Direct Source for the text below
Identifying the order of differencing and the constant:
- Rule 1: If the series has positive autocorrelations out to a high number of lags (say, 10 or more), then it probably needs a higher order of differencing.
- Rule 2: If the lag-1 autocorrelation is zero or negative, or the autocorrelations are all small and patternless, then the series does not need a higher order of differencing. If the lag-1 autocorrelation is -0.5 or more negative, the series may be overdifferenced. BEWARE OF OVERDIFFERENCING.
- Rule 3: The optimal order of differencing is often the order of differencing at which the standard deviation is lowest. (Not always, though. Slightly too much or slightly too little differencing can also be corrected with AR or MA terms. See rules 6 and 7.)
- Rule 4: A model with no orders of differencing assumes that the original series is stationary (among other things, mean-reverting). A model with one order of differencing assumes that the original series has a constant average trend (e.g. a random walk or SES-type model, with or without growth). A model with two orders of total differencing assumes that the original series has a time-varying trend (e.g. a random trend or LES-type model).
- Rule 5: A model with no orders of differencing normally includes a constant term (which allows for a non-zero mean value). A model with two orders of total differencing normally does not include a constant term. In a model with one order of total differencing, a constant term should be included if the series has a non-zero average trend.
Identifying the numbers of AR and MA terms:
- Rule 6: If the partial autocorrelation function (PACF) of the differenced series displays a sharp cutoff and/or the lag-1 autocorrelation is positive–i.e., if the series appears slightly “underdifferenced”–then consider adding one or more AR terms to the model. The lag beyond which the PACF cuts off is the indicated number of AR terms.
- Rule 7: If the autocorrelation function (ACF) of the differenced series displays a sharp cutoff and/or the lag-1 autocorrelation is negative–i.e., if the series appears slightly “overdifferenced”–then consider adding an MA term to the model. The lag beyond which the ACF cuts off is the indicated number of MA terms.
- Rule 8: It is possible for an AR term and an MA term to cancel each other’s effects, so if a mixed AR-MA model seems to fit the data, also try a model with one fewer AR term and one fewer MA term–particularly if the parameter estimates in the original model require more than 10 iterations to converge. BEWARE OF USING MULTIPLE AR TERMS AND MULTIPLE MA TERMS IN THE SAME MODEL.
- Rule 9: If there is a unit root in the AR part of the model–i.e., if the sum of the AR coefficients is almost exactly 1–you should reduce the number of AR terms by one and increase the order of differencing by one.
- Rule 10: If there is a unit root in the MA part of the model–i.e., if the sum of the MA coefficients is almost exactly 1–you should reduce the number of MA terms by one and reduce the order of differencing by one.
- Rule 11: If the long-term forecasts* appear erratic or unstable, there may be a unit root in the AR or MA coefficients.
Identifying the seasonal part of the model:
- Rule 12: If the series has a strong and consistent seasonal pattern, then you must use an order of seasonal differencing (otherwise the model assumes that the seasonal pattern will fade away over time). However, never use more than one order of seasonal differencing or more than 2 orders of total differencing (seasonal+nonseasonal).
- Rule 13: If the autocorrelation of the appropriately differenced series is positive at lag s, where s is the number of periods in a season, then consider adding an SAR term to the model. If the autocorrelation of the differenced series is negative at lag s, consider adding an SMA term to the model. The latter situation is likely to occur if a seasonal difference has been used, which should be done if the data has a stable and logical seasonal pattern. The former is likely to occur if a seasonal difference has not been used, which would only be appropriate if the seasonal pattern is not stable over time. You should try to avoid using more than one or two seasonal parameters (SAR+SMA) in the same model, as this is likely to lead to overfitting of the data and/or problems in estimation.
A caveat about long-term forecasting in general: linear time series models such as ARIMA and exponential smoothing models predict the more distant future by making a series of one-period-ahead forecasts and plugging them in for unknown future values as they look farther ahead. However, the models are identified and optimized based on their one-period-ahead forecasting performance, and rigid extrapolation of them may not be the best way to forecast many periods ahead (say, more than one year when working with monthly or quarterly business data), particularly when the modeling assumptions are at best only approximately satisfied (which is nearly always the case). If one of your objectives is to generate long-term forecasts, it would be good to also draw on other sources of information during the model selection process and/or to optimize the parameter estimates for multi-period forecasting if your software allows it and/or use an auxiliary model (possibly one that incorporates expert opinion) for long-term forecasting.
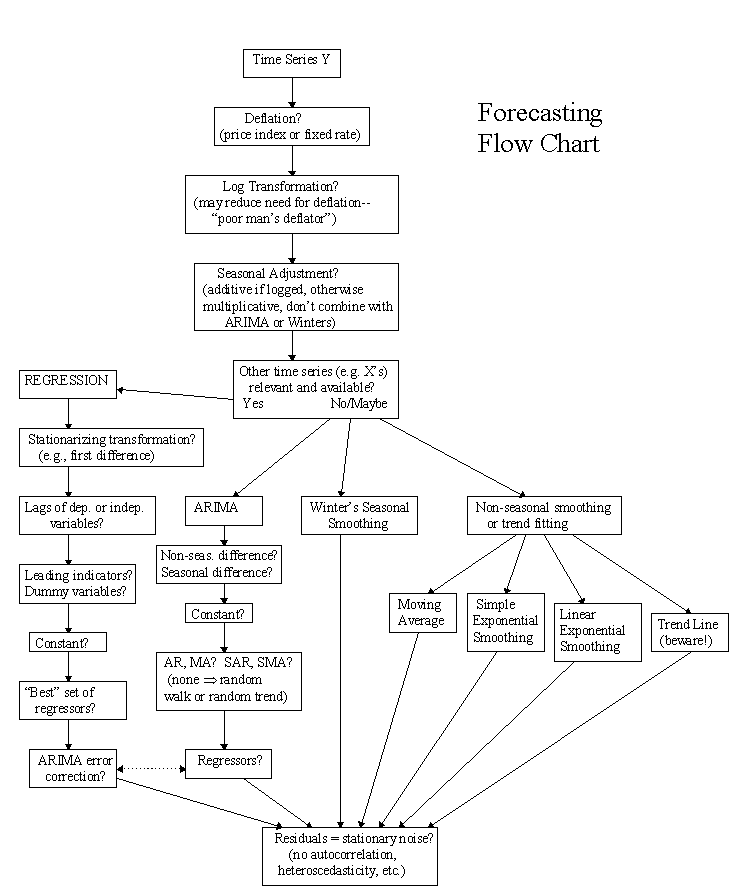
6. Choosing the right forecasting model
Steps in choosing a forecasting model
Deflation?
If the series show inflationary growth. Help to account for the growth pattern and reduce heteroscedasticity in the residuals.
Logarithm transformation?
If the series shows compound growth and/or a multiplicative seasonal pattern, a logarithm transformation may be helpful in addition to or lieu of deflation. Logging the data will not flatten an inflationary growth pattern, but it will straighten it out it so that it can be fitted by a linear model (e.g., a random walk or ARIMA model with constant growth, or a linear exponential smoothing model).
Convert multiplicative seasonal patterns to additive patterns, so that if you perform seasonal adjustment after logging, you should use the additive type.
Another important use for the log transformation is linearizing relationships among variables in a regression model
Seasonal adjustment?
If the series has a strong seasonal pattern which is believed to be constant from year to year, seasonal adjustment may be an appropriate way to estimate and extrapolate the pattern.
The advantage of seasonal adjustment is that it models the seasonal pattern explicitly, giving you the option of studying the seasonal indices and the seasonally adjusted data.
The disadvantage is that it requires the estimation of a large number of additional parameters (particularly for monthly data), and it provides no theoretical rationale for the calculation of “correct” confidence intervals
Independent variables?
If there are other time series which you believe to have explanatory power with respect to your series of interest (e.g., leading economic indicators or policy variables such as price, advertising, promotions, etc.)
Smoothing, averaging, or random walk?
If you have chosen to seasonally adjust the data–or if the data are not seasonal to begin with–then you may wish to use an averaging or smoothing model to fit the nonseasonal pattern which remains in the data at this point
If smoothing or averaging does not seem to be helpful–i.e., if the best predictor of the next value of the time series is simply its previous value–then a random walk model is indicated.
Brown’s linear exponential smoothing can be used to fit a series with slowly time-varying linear trends, but be cautious about extrapolating such trends very far into the future.
Holt’s linear smoothing also estimates time-varying trends, but uses separate parameters for smoothing the level and trend, which usually provides a better fit to the data than Brown’s model.
Winters Seasonal Exponential Smoothing?
Extension of exponential smoothing that simultaneously estimates time-varying level, trend, and seasonal factors using recursive equations. (Thus, if you use this model, you would not first seasonally adjust the data.)
The Winters seasonal factors can be either multiplicative or additive: normally you should choose the multiplicative option unless you have logged the data. Although the Winters model is clever and reasonably intuitive, it can be tricky to apply in practice: it has three smoothing parameters–alpha, beta, and gamma–for separately smoothing the level, trend, and seasonal factors, which must be estimated simultaneously.
ARIMA?
If you do not choose seasonal adjustment (or if the data are non-seasonal), you may wish to use the ARIMA model framework.
ARIMA models are a very general class of models that includes random walk, random trend, exponential smoothing, and autoregressive models as special cases.
The conventional wisdom is that a series is a good candidate for an ARIMA model if:
- (i) it can be stationarized by a combination of differencing and other mathematical transformations such as logging, and
- (ii) you have a substantial amount of data to work with: at least 4 full seasons in the case of seasonal data. (If the series cannot be adequately stationarized by differencing–e.g., if it is very irregular or seems to be qualitatively changing its behavior over time–or if you have fewer than 4 seasons of data, then you might be better off with a model that uses seasonal adjustment and some kind of simple averaging or smoothing.)
Steps
- Determine the appropriate order of differencing needed to stationarize the series and remove the gross features of seasonality
- Determine whether to include a constant term in the model: usually you do include a constant term if the total order of differencing is 1 or less, otherwise you don’t
- Choose the numbers of autoregressive and moving average parameters (p, d, q, P, D, Q) that are needed to eliminate any autocorrelation that remains in the residuals of the naive model (i.e., any correlation that remains after mere differencing).
It is usually better to proceed in a forward stepwise rather than backward stepwise fashion when tweaking the model specifications: start with simpler models and only add more terms if there is a clear need.
Forecasting Flow Chart
Source: https://people.duke.edu/~rnau/411flow.gif
Automatic Forecasting Software
WARNING: Properly used, and guided by experience with “manual” model-fitting, the best of such software can put more data-analysis power at your fingertips and speed up routine forecasting applications. Carelessly used, it merely allows you to foul things up in a bigger way, obtaining results without insight while getting a false sense of security that “the computer knows best.” Automatic forecasting software is a complement to, not a substitute for, your own forecasting expertise.
How to avoid trouble: principles of good data analysis
Source: https://people.duke.edu/~rnau/notroubl.htm
- Do some background research before running any numbers. Be sure you understand the objective, the theory, the jargon, and the conventional wisdom. Ask others what they know about the problem. Do more of the same web-searching that brought you to this site, and be critical of everything you find.
- Be thorough in your search for data. In the end, your forecasts will contain no information that is not hidden in it somewhere. In some cases (say, designed experiments) the data may be limited in scope and already in hand, but in many cases it will be up to you to identify and collect it, and this may the most important and time-consuming part of the project. We now live in the era of “megadata”, but often the data that you need is not so easy to find.
- Check the data carefully once you have it: make sure you know where the numbers came from, what they mean, how they were measured, how they are aligned in time, and whether they are accurate. A lot of cleaning and merging of data may be needed before any analysis can begin, and you should know how to do it. You may find that you need yet-more-data or better-quality data to answer the key questions, and sometimes the most useful lesson is that the organization will need to do a better job of managing its data in the future.
- Use descriptive, self-explanatory names for your variables (not Y’s and X’s or cryptological character strings) so that their meaning and units are clear and so that your computer output is self-documenting to the greatest extent possible.
- Once you begin your analysis, follow good modeling practices: perform exploratory data analysis, use appropriate model types, interpret their estimated parameters, check their residual diagnostics, question their assumptions, and validate them with out-of-sample testing where possible.
- Make effective use of statistical graphics in your own analysis and in your presentation of your results to others, and follow rules of good graphics. Among other things: graphs should be self-explanatory and not contain visual puzzles, they should have titles that are specific to the variables and models, axes should be well-scaled and well-labeled, the data area should have a white background, grid lines (if any are needed) should not be too dark, point and line widths should be sized appropriately for the density of the data, self-promoting artwork (3-D perspective, etc.) should be avoided, and above all, the data should tell its own story.
- Keep in mind that not all relationships are linear and additive, not all randomness is normally distributed, and regression models are not magic boxes that can predict anything from anything. Be aware that it may be necessary to transform some of your variables (through deflating, logging, differencing, etc.) in order to match their patterns up with each other in the way that linear models require.
- When comparing models, focus on the right objectives, which are usually making the smallest possible errors in the future and deriving inferences that are genuinely useful for decision making. A good fit to past data does not always guarantee an equally good prediction of what will happen next, and statistical significance is not always the same as practical significance.
- Other things being equal, KEEP IT SIMPLE and intuitively reasonable. If others don’t understand the model, they may not use it, and perhaps they shouldn’t: simple models often outperform complicated models in practice.
- If you use automatic forecasting software, you are still responsible for the model that is chosen, and you should be able to explain its logic to others. The availability of such software does not make it unnecessary to know how the models work. Rather, it makes that knowledge even more important. Be aware that in automatic rankings of models, there may be only tiny differences in error stats between the winner and its near competitors, and you may need to take other factors into account in your final selection, such as simplicity, clarity, and intuition. And again, your software cannot make something out of nothing. If your data is not informative or not properly organized to begin with, automatic methods will not turn it into gold.
- Leave a paper trail, i.e., keep well-annotated records of your model-fitting efforts. Don’t just save your computer files: write up notes as you go along. Someone else (who may be a sharp-penciled auditor or perhaps only yourself 12 months hence) may need to reconstruct what you did and why you did it. Intelligent naming of variables and labeling of tables and charts will make this easier.
- Neither overstate nor understate the accuracy of your forecast, and do not merely give a point value. Always report standard errors and/or confidence intervals.
- If different forecasting approaches lead to different results, focus on differences in their underlying assumptions, their sources of data, their intrinsic biases, and their respective margins for error. Don’t just argue over the outputs. Look for opportunities to combine independent viewpoints and information.
- After all has been said, if you believe your model is more useful and better supported than the alternatives, stand up for it. The future may still be very uncertain, but decisions ought to be based on the best understanding of that uncertainty. If you don’t have confidence in your model (or anyone else’s), admit it, and keep digging.

